고정 헤더 영역
상세 컨텐츠
본문
https://www.youtube.com/watch?v=7MdQ-UAhsxA&list=PL_iJu012NOxehE8fdF9me4TLfbdv3ZW8g&index=4
본 필기노트는 위 영상을 바탕으로 합니다.
다시 강화학습은 Expacted Return을 Maximize하는 것이라 언급.
State value function (상태 가치 함수, V)
지금부터 기대되는 return. (지금 Stae 부터)
지금 state에 대한 value, 가치를 매겨주는 것

일반적으로 x에 대한 기댓값은 왼쪽과 같이 나타낸다.
말로 풀자면, x의 결괏값 f(x)의 기댓값은 f(x)와 x가 일어난 확률 p(x)의 곱을 적분한 것과 같다.
이를 바탕으로 현재 state S_(t)에 대하여 수식으로 나타낸다면,

여기서의 G_(t)는 Return값.
지난번에 G_(t)를 다음과 같이 정의했다.

상태가치함수 V는 t부터 ∞까지
t번째 state에서 Expected Return값과,
t번째 state에서의 다른 action과 state의 조건부확률을 곱한 것의 적분값이 된다.
그러니까 조금 더 쉽게 설명하자면.....
현재 State의 Expected Return값 * 현재 State 이후의 미래에 action과 그에 따른 State의 확률
그리고 그것의 적분 값이다.
action을 취하면서 State가 변화하고 그에따른 루트가 만들어질 것인데,
그 루트가 일어날 확률과 그 루트의 Expected Return값을 곱해주겠다.
그리고 그것을 적분해주겠다.(라고 이해했습니다.)
그리고 Sate value function, 상태가치함수를 maximize 하는 policy가 Optimal policy이다.
Action value function (행동 가치 함수, Q)
이전 Q-learning에서 사용했던 Q값.
그렇게 행동에 value를 매겨나가는 것.
지금 행동으로부터 기대되는 return.
그래서 Q값은 아래와 같이 정의할 수 있다.
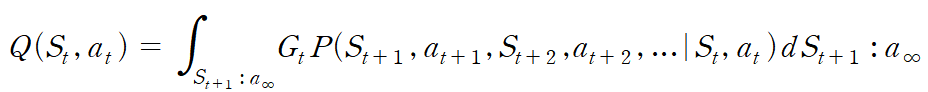
상태가치함수는 지금 State에서 기대되는 return이었지만,
행동가치함수는 지금 action에서 기대되는 return이므로 Q의 input에는 action과 해당 State가 포함된다.
(State 없이 action은 없으니까)
S_(t+1), a_(t+1)부터 무한대까지의 State와 action의 나열이 발생할 확률과 그에 따른 return값을 곱해 적분한다.
비슷해 보이지만 다른 두 가지.
Bellman equation 벨만 방정식
앞서 State value function 상태가치함수를 정의한 식을 사용하는데, 알아두어야 할 것이 있다.

x,y의 확률 P(x,y)는 왼쪽과 같이 표현할 수 있다.
y가 주어졌을 때, x의 확률 * y의 확률.
'Study > 강화학습' 카테고리의 다른 글
| 강화학습 필기노트 - 3 Markov Decision Process (MDP) && Policy (0) | 2023.01.10 |
|---|---|
| 강화학습 필기노트 - 2 Q-learning (0) | 2023.01.10 |
| 강화학습 필기노트 - 1 Introduction (0) | 2023.01.01 |





댓글 영역