고정 헤더 영역
상세 컨텐츠
본문
https://www.youtube.com/watch?v=3Ch14GDY5Y8&list=PL_iJu012NOxehE8fdF9me4TLfbdv3ZW8g&index=2
본 필기노트는 위 영상을 바탕으로 합니다.
위 영상에서는 강화학습의 Q-learning 알고리즘을 '맛집 찾기' 과정에 비유하여 설명합니다.
Greedy Action

각각의 칸을 state로 보고 칸을 이동하는 행위를 action으로 볼 때, 위 그림처럼 표현할 수 있다.

각 state에서 취할 수 있는 action에 따라 Q값을 가진다.
이 Q값이 큰 action을 따라 움직이는 것이 Greedy Action이다.
모든 action의 최초 Q값은 0으로 초기화된다.
이때, 첫번째 Episode 시행에서는 Q값이 모두 0이기 때문에, 랜덤한 action을 수행한다.

그리고, 목표지점에 다다랐을때, 마지막 action에 Q값을 변경한다.

다음 Episode에서 이전에 Q값이 변경된 state로 이동하는 action이 수행된다면,
이때 이동한 state의 최대 Q값이 1임을 알았으니 직전 action의 Q값을 변경해 준다.
왜냐? 이 action을 취하면 다음 state의 최대 Q값이 1임을 알았으니까!
다만! 무조건 Q값이 변경된 state로 가는 action을 취하는 것이 아니라! 랜덤시행을 거쳤을 때,
해당 action이 Q값이 변경된 state로 갔을 때에 바뀐다는 것이다.
하지만 이런 Greedy Action만을 반복한다면...

무수히 많은 Episode를 지나도 계속해서 같은 루트만을 지나가게 된다.
왜냐? Greedy Action은 항상 Q값이 최대인 action을 취하기 때문이다.
더 좋은 길이 있을 수 있지 않을까?
그래서 탐험 Exploration을 한다.
Exploration
이 exploration은 ε - Greedy (입실론 그리디)를 사용한다.
ε 값을 0 ~ 1 (0 ~ 100%)로 설정하여, 전체 시행 중 ε 만큼은 Q값, Greedy와 상관없이 랜덤한 action을 취한다.
그래서 이렇게 움직이는 것을 Exploration, Greedy에 따라 움직이는 방법을 Exploitation이라 한다.
이러한 Exploration의 장점!

1. 새로운 path를 찾을 수 있다!
2. 새로운 맛집을 찾을 수 있다! → 무슨 말일까?
우리가 강화학습을 사용할 때는, 모든 상황을 알고 있지 않은 경우다.
예를 들어, 알파고는 대국을 승리하는 포진 하나만을 따르지 않는다. 바둑에는 여러 가지 승리의 경우가 있다.
결국 우리가 목표하는 바를 이룰 수 있는 다른 경우를 찾아낼 수 있다는 것이다!!
다만, 너무 Exploration에만 의존하는 경우에는 Greedy를 이용하지 않기에 학습에 문제가 생길 수 있다.
그래서 사용하는 방식이 (Decaying) ε - Greedy이다.
무엇이냐? ε 을 처음에 설정해 두고, 매 episode를 거치면서 0으로 줄여나가는 것.
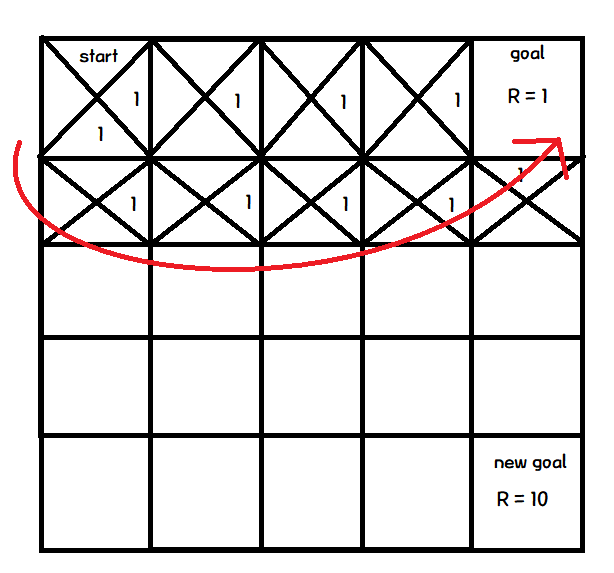
그렇게 새로운 path를 찾았다.
하지만, 여기서 생기는 문제점.
각 action에 할당된 Q값이 1이기 때문에, 어떤 path가 더 좋은지 판단할 수 없다는 것.
그래서 Q값으로 1 대신에 γ (감마)를 사용한다.
Discount Factor
γ 는 0과 1 사이에 존재하는 값.

그래서 1 대신 γ를 사용한다면 위와 같이 나타낼 수 있다.
이 경우에 Greedy Action은 γ가 0과 1 사이의 값이므로 지수가 작은 값을 선택하게 된다.
이 방법을 Discount factor를 사용한다고 한다.
Discount factor의 장점
1. 효율적인 path를 찾게 해 준다.
2. 현재 reward와 미래 reward에 대한 집중도를 나누어 줄 수 있다.
γ를 크게 가져가는 경우에, 예를 들어 0.9로 설정한다면

현재 action의 기대 reward값이 높기 때문에 현재의 reward에 집중하게 된다.
반대로 γ를 작게 가져가는 경우에는

당장의 action에 기대 reward값이 낮기 때문에 미래 reward에 집중하게 된다.
라고는 하는데 아직 정확히 이해는 못하겠네요...
Q - Update
앞서 action의 Q값은 다음 state의 maxQ값에 γ를 곱하는 것으로 나타냈지만, 사실은 조금 다르다.

t번째 state의 Q값을 대입할 때, 위의 식을 따른다.
α변수는 0과 1 사이에 위치하며 기존 값에서 새로운 값을 얼마나 받아들일지를 결정한다.
그리고 새로운 값에는
1. 다음 state가 목표지점인 경우
이 경우에는 직접적인 Reward가 존재한다.
허나, t+1 번째 state의 Q가 존재하지 않기 때문에 maxQ 값은 0이 된다.
2. 다음 state가 목표지점이 아닌 경우
이 경우는 직접적인 Reward는 존재하지 않는다.
그러나, 다음 State가 해당하는 maxQ값을 가진다.
이것을 문장으로 정리하자면,
t번째 State에 값을 넣을 때는 α값에 따라 기존 값과 새로운 값의 비율을 정하며,
t+1번째 State가 목표지점인 경우 αRt, 아닌 경우 αγmaxQ 가 새로운 값이 된다.
이런 방식은 Q값을 한 번에 업데이트하는 게 아니라 천천히 업데이트된다는 것을 의미한다
제가 듣고 이해한 내용을 바탕으로 작성한 글인데... 틀린 내용이 있다면 댓글로 남겨주시면 감사합니다.
'Study > 강화학습' 카테고리의 다른 글
| 강화학습 필기노트 - 4 상태 가치 함수 V, 행동 가치 함수 Q, 벨만 방정식 Bellman equation (0) | 2023.01.12 |
|---|---|
| 강화학습 필기노트 - 3 Markov Decision Process (MDP) && Policy (0) | 2023.01.10 |
| 강화학습 필기노트 - 1 Introduction (0) | 2023.01.01 |





댓글 영역